Room acoustics
Much has been written in the popular and professional audio press about the acoustic treatment of rooms. The purpose of such treatment is to allow us to hear more of the loudspeaker and less of the room. I am convinced that a properly designed sound system can perform well in a great variety of rooms and requires only a minimum of room treatment if any at all.
To understand this claim let's look at the typical acoustic behavior of domestic size listening rooms, which have linear dimensions that are small compared to the 17 m wavelength of a 20 Hz bass tone, but are acoustically large when compared to a 200 Hz or 1.7 m wavelength midrange tone (G1 on the piano keyboard).
Below 200 Hz the acoustics of different locations in the room are dominated by discrete resonances. Above 200 Hz these resonances become so tightly packed in frequency and space that the room behaves quite uniformly and is best described by its reverberation time RT60 (Ref. 1).
Room treatment can be very effective above 200 Hz, but the same result may be obtained more aesthetically with ordinary furnishings, wall decoration, rugs on the floor and the variety of stuff we like to surround ourselves with. How much treatment is needed, or how short the reverberation time should be, depends on the polar radiation characteristics of the loudspeaker. For my open baffle speaker designs a room becomes too dead when its RT60 falls below 500 ms.
We can think of sound as propagating like a light ray. Thus, we can use a mirror to find the region on the side wall or ceiling where sound from the speaker might be reflected towards the preferred listening location. It depends on driver, crossover and baffle design, i.e. the polar radiation pattern, whether the region so found is illuminated by sound to any significant degree. If so, then a variety of commercial surface coverings are available to scatter and/or absorb the offending reflection.
The acoustically most problematic frequency range is below 200 Hz, because of the spatially and frequency wise irregular distribution of room resonances. Many computer programs have been written that calculate the resonant modes of a given room and recommend optimum loudspeaker and listener placements. Usually, real rooms are much more complex than the calculated models. Walls are not infinitely stiff, rooms have windows, doors, openings, suspended floors or ceilings, etc. In addition, it is the polar pattern and the acoustic source impedance of the given loudspeaker that determines which of the potential room modes are actually excited and to which degree. The usefulness of such programs is marginal at best. Likewise, recommended proportions for room length, width and height should not be taken more seriously than other proportions that may be based on visual aesthetics.
The conventional closed or vented box design, that is used for the majority of loudspeakers on the market, contributes significantly to the room problems below 200 Hz. These designs are omni-directional radiators and they tend to excite a maximum number of room resonances, particularly when located in room corners. While this adds to the perceived bass output at certain frequencies, it can lead to a falsification of the recorded material, namely when the room resonance decays more slowly than the original sound. In general, the low frequency response of omni-directional speakers in small rooms is quite non-uniform. Attempts to treat the room with absorbers will make only marginal differences unless very many absorbers or large absorbing surfaces are used. It is best to attenuate peaks in the bass response with parametric equalization. Holes in the response cannot be filled in (Ref. 1).
By far the most uniform response in the range below 200 Hz is obtained with an open-baffle, dipole or figure-of-eight radiating source. Because of its directionality, the dipole excites far fewer room resonances than an omni-directional source. The difference in bass reproduction is startling at first, because we are so used to hearing the irregular and booming bass of the typical box speaker in acoustically small rooms. Quickly one learns to recognize the distortion of this combination and it becomes intolerable.
For evaluating a given room and loudspeaker combination a CD is available. It contains unique sound tracks to identify room resonances and their effect upon the clarity of sound reproduction. Many of the tests require no instrumentation other than your ears.
Loudspeaker directivity and room response
When a loudspeaker is placed in a room we hear both its direct sound, i.e. the sound which arrives via the shortest path, and the room sound due to the resonances, reverberation and reflections caused by the boundaries of the room and the objects in it. The two sounds superimpose and influence our perception of timbre, timing and spatial location of the virtual sound source. Thus, the off-axis radiation of the speaker has great influence on the naturalness of sound reproduction even when you listen on-axis and the more so, the further you sit away from the speaker.
Two basic and fundamentally different sources of sound are
the monopole and the dipole radiator. The ideal monopole is an acoustically
small pulsating sphere, and the ideal dipole is a back and forth oscillating
small sphere. The monopole radiates uniformly into all directions, whereas the
dipole is directional with distinct nulls in the plane vertical to its axis of
oscillation. The 3-dimensional radiation or polar pattern of the monopole is
like the surface of a basket ball, the dipole's is like two ping-pong balls
stuck together. At +/-45 degrees off-axis the dipole response is L = cos(45) =
0.7 or 3 dB down, the monopole is unchanged with L = 1.
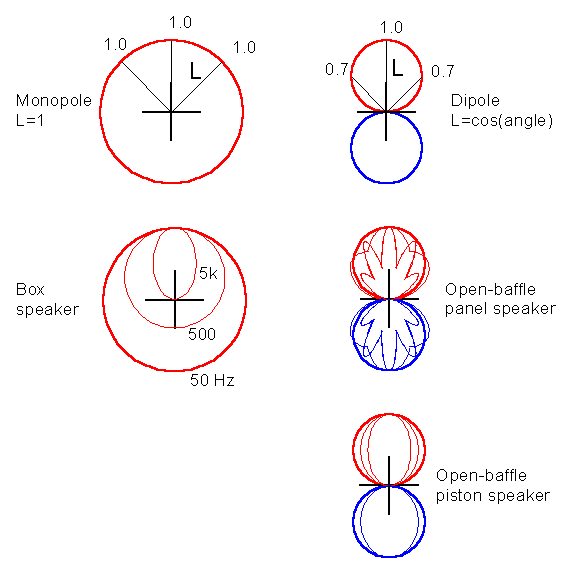
The graph above shows characteristic radiation patterns of
different sound sources for very low, mid and high frequencies and with flat
on-axis response.
Practical loudspeakers
are neither pure monopoles nor pure dipoles except at low frequencies where the
acoustic wavelengths are large compared to the cabinet dimensions.
The ideal monopole is omni-directional at all frequencies. Very few speaker designs on the consumer market approach this behavior. This type of speaker illuminates the listening room uniformly and the perceived sound is strongly influenced by the room's acoustic signature. The result can be quite pleasing, though, because a great deal of acoustic averaging of the sound radiated into every direction takes place. The speakers tend to disappear completely in the wide sound field. Unfortunately, the direct sound is maximally masked by the room sound and precise imaging is lost, unless the listening position is close to the speakers.
The typical box speaker, whether vented, band-passed or closed, is omni-directional at low frequencies and becomes increasingly forward-directional towards higher frequencies. Even when flat on-axis, the total acoustic power radiated into the room drops typically 10 dB (10x) or more between low and high frequencies. The uneven power response and the associated strong excitation of low frequency room modes contributes to the familiar (and often desired :-( ) generic box loudspeaker sound. This cannot be the avenue to sound reproduction that is true to the original.
The directional response of the ideal dipole is obtained with open baffle speakers at low frequencies. Note, that to obtain the same on-axis sound pressure level as from a monopole, a dipole needs to radiate only 1/3rd of the monopole's power into the room. This means 4.8 dB less contribution of the room's acoustic signature to the perceived sound. It might also mean 4.8 dB less sound for your neighbor, or that much more sound to you. Despite this advantage dipole speakers are often not acceptable, because they tend to be constructed as physically large panels that interfere with room aesthetics, and they seem to suffer from insufficient bass output, critical room placement and a narrow "sweet spot".
These claims are true to varying degree depending on the specific design of a given panel loudspeaker. Because of the progressive acoustic short circuit between front and rear as the reproduced signal frequency decreases, the membrane of an open-baffle speaker has to move more air locally than the driver cone of a box speaker for the same SPL at the listening position. This demands a large radiating surface area, because achievable excursions are usually small for electrostatic or magnetic panel drive. The obtained volume displacement limits the maximum bass output. Non-linear distortion, though, is often much lower than for dynamic drivers. Large radiating area means that the panel becomes multi-directional with increasing frequency which contributes to critical room placement and listening position.
If the open-baffle speaker is built with conventional cone
type dynamic drivers of large excursion capability, then adequate bass output
and uniform off-axis radiation are readily obtainable in a package that is more
acceptable than a large panel, though not as small as a box speaker. Such
speakers were built by Audio Artistry Inc. and a DIY project is described on
this web site in the PHOENIX pages. This type of speaker has a much more
uniform power response than the typical box speaker. Not only is its bass output
in proportion to the music, because room resonance contribution is greatly
reduced, but also the character of the bass now sounds more like that from real
musical instruments. My hypothesis is that three effects combine to produce
the greater bass clarity:
1 - An open baffle, dipole speaker has a figure-of-eight radiation pattern and
therefore excites fewer room modes.
2 - Its total radiated power is 4.8 dB less than that of a monopole for the same
on-axis SPL. Thus the strength of the excited modes is less.
3 - A 4.8 dB difference in SPL at low frequencies is quite significant, due to
the bunching of the equal loudness contours at low frequencies, and corresponds
to a 10 dB difference in loudness at 1 kHz.
Thus, bass reproduced by a dipole would be less masked by the room, since a
dipole excites fewer modes, and to a lesser degree, and since the perceived
difference between direct sound and room contribution is magnified by a
psychoacoustic effect.,
The off-axis radiation behavior of a speaker determines the degree to which speaker placement and room acoustics degrade the accuracy of the perceived sound. Worst in this respect is the typical box speaker, followed by the large panel area dipole and the truly omni-directional designs. Least affected is the sound of the open-baffle speaker with piston drivers. (Ref.1)
Often concern is expressed over the fact that the rear radiation from a dipole is out of phase with the front radiation, and that thus any sound reflected from a wall behind the speaker would cancel sound coming from the front of the speaker. Cancellation can only occur when direct and reflected sounds are exactly of opposite phase (180 degrees) and of the same strength. Since direct and reflected sounds travel paths of different length, they undergo different amounts of phase shift. Thus, the phase and magnitude conditions for cancellation are given only at certain frequencies, if at all. At some other frequencies direct and reflected sounds will add. The same also applies to a monopole speaker in front of a wall. The only difference is in the frequencies for which addition and subtraction occur. The best remedy is to move the speaker away from the wall, or to make the wall as sound absorptive or diffusive as possible. (FAQ31)
Room reverberation time T60
Reverberation time is the single most important parameter describing a room's acoustic behavior. The following discussion might get a little technical but will illustrate how sound builds up and decays in a room and the effect it has upon clarity of reproduction.
Sound waves between two walls
Take the example of a speaker in a wall and a second wall at distance L in
front of it. As the cone vibrates it will send out an acoustic wave which gets
reflected back by the second wall, returns to the first wall, gets reflected
again back to the second wall and so on. If the frequency of vibration is such
that the distance L corresponds to half of a wavelength, then the cone movement
is in phase with the reflected wave and the sound pressure keeps building up.
Eventually an equilibrium is reached between the energy supplied by the cone
movement and the energy absorbed by the two walls and the air in between.
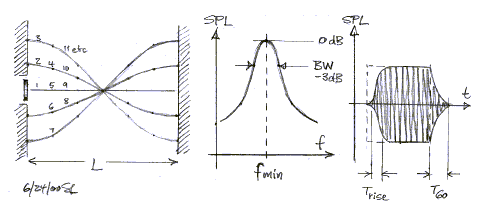
This is a standing wave resonance or mode condition and if we change the frequency of cone vibration, we trace out the resonance curve that is typical for any simple system containing mass, compliance and energy loss. As frequency is increased another resonance occurs when L equals to a full wavelength, to 3/2 wavelengths, 4/2 and so on. The lowest possible frequency is
fmin = c / (2 L) Hz, where c=343 m/s (1)
If the excitation is applied as a step function, then the sound pressure will rise from 10% to 90% of its steady-state level within a time
Trise = 0.7 / BW (2)
where BW is the width of the resonance curve in Hz at the half power (-3 dB) level. The SPL will decay to one millionth (-60 dB) of its full level after a time
T60 = 2.2 / BW (3)
The quality factor or Q of the resonance is
Q = n fmin / BW (4) with n = 1, 2, 3, etc.
Example 1
L=25 ft (7.63 m), then fmin =
343/(2*7.63) = 22.5 Hz and no resonance below this frequency. The next higher
resonance will be at 45 Hz, then 67.5 Hz, 90 Hz, 112.5 Hz and so on.
If we had measured Trise = 202 ms at 45 Hz,
then from (2) BW = 0.7/0.202 = 3.5 Hz and T60 = 2.2/3.5 = 630
ms from (3).
Q = 45/3.5 = 12.9 and if T60 stays constant with increasing
frequency, then Q increases, for example Q = 112.5/3.5 = 32.1
Standing waves in a rectangular, rigid room
In a rectangular room we have six surfaces and the number of possible
standing waves is much larger than for the two wall example. The frequencies at
which they can occur are calculated from
f = ( c / 2 ) [ ( l / L )2 + ( w / W )2 + ( h / H )2 ]1/2 [Hz] (5)
l, w, h = 0, 1, 2, 3 etc.
See modes1.xls, a spreadsheet for calculating and plotting room modes and other room parameters discussed here.
At frequencies below the lowest room resonance the sound
pressure will increase at a rate of 12 dB/oct for a closed box speaker that is
flat under anechoic conditions, assuming that the room is completely closed and
its surfaces are rigid. This case has some significance for the interior of
automobiles. Under the same circumstances the sound from a dipole speaker will
stay flat.
Domestic listening spaces are seldom completely closed, nor are sheet rock walls
rigid, making a prediction of very low frequency in-room response extremely
difficult.
Note: Calculations of room modes, though popular, are not practical for predicting optimum speaker placement or listener position. For this one would need to calculate the transfer function between speaker and listener. The transfer function is related to the room modes, but much more difficult to determine. Never-the-less, room mode calculations are often invoked to predict "optimum" room dimensions. They fail to take into account any specifics about speaker placement, source directivity and source type (monopole vs. dipole) that determine which modes are excited, and in combination with the absorption properties of different room surfaces, to which degree these resonances build up. Some people think that by making the room other than rectangular or using curved surfaces, that they can eliminate standing waves. They merely change frequencies, shift their distribution and make their calculation a lot more difficult.
Room modes can be identified by peaks and dips in the frequency response of the acoustic transfer function between speaker and listening position, though only at low frequencies (<150 Hz) where their density is not too high. Such measurements are location dependent and are difficult to interpret as to their audible effect. Listening to a multi-burst test signal at different frequencies gives audible indication of which room locations and frequency regions suffer the greatest degradation in the articulation of bass sounds (Ref.1). With this information in hand it is then possible to identify and electronically equalize the worst offenders in the acoustic transfer function response.
Several room parameters can be calculated that give insight into the general behavior of a closed space.
The number of modes N between zero and a given upper frequency limit fm can be estimated (H. Kuttruff, Room Acoustics, 1991) from
N = (4 p / 3) V (fm/c)3 + (p / 4) S (fm /c)2 + (1 / 8) Le (fm /c) (6)
where
V = L W H [m3]
S = 2 ( L W + L H + W H ) [m2]
Le = 4 ( L + W + H ) [m]
The number of modes increases very rapidly with frequency and they move ever more closely together. Their average separation at fm is
df = c3 / ( 4 p V fm2 ) [Hz] (7)
Example 2
Take a room with L = 25', W = 16' and H = 9' (7.62m x 4.88m x 2.74m), then
V = 3600 ft3 = 102 m3
S = 1537 ft2 = 143 m2
Le = 200 ft = 61 m
Below fm = 100 Hz, 200, 300 and 400 Hz the number of modes N and
their average separation df
at fm are respectively
| fm | N | df |
| 100 Hz | 22 | 3.2 Hz |
| 200 Hz | 126 | 0.8 Hz |
| 300 Hz | 375 | 0.4 Hz |
| 400 Hz | 832 | 0.2 Hz |
If we assume that the modes in this room decay at T60 = 630 ms, then each resonance occupies a 3 dB bandwidth BW = 3.5 Hz from (3) above. Somewhere between 100 Hz and 200 Hz the average separation df between modes is 1.2 Hz and thus 3 modes fall within the 3.5 Hz bandwidth resulting from T60. This occurs at fs = 157 Hz as calculated from the simple formula for 3 overlapping modes per BW:
fs = 2000 ( T60 / V )1/2 [Hz] (8)
The frequency fs is also called the Schroeder frequency and denotes approximately the boundary between reverberant room behavior above and discrete room modes below.
The sound decay time or reverberation time T60 is related to the average wall absorption coefficient a by Sabine's formula
T60 = 0.163 V / ( S a ) [s] (9)
a = 18% for the Example 2 room with T60 = 630 ms.
A CD containing unique test signals is available. It allows to evaluate the effect of room modes upon the clarity of sound reproduction.
Reverberation distance
When we consider radiation in the reverberant frequency range above 149 Hz,
the sound at the listening position is composed of the direct sound from the
source and the reverberant sound that is more or less uniformly distributed in
the room. The direct sound pressure level decreases inversely to distance from
the source and will equal the reverberant sound pressure at distance xr.
The ‘reverberation distance’ xr (also called 'critical distance')
is calculated from
xr = 0.1 ( G V / (p T60) )1/2 [m] (10)
where the directionality gain G is unity for a monopole and G = 3 for a dipole radiator. A dipole, thus, has a 31/2 = 1.73 times larger reverberation distance.
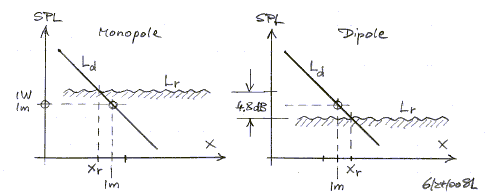
A typical reverberation distance is actually quite small, 0.72 m (2.4 ft) for the monopole and 1.24 m (4.1 ft) for the dipole in the example room. Never-the-less, the ratio of direct sound Ld to reverberant sound pressure level Lr is 4.8 dB greater for the dipole than for a monopole with the same direct sound output. Thus, at 3 m distance from the source, the direct sound would be 20*log(3/0.72) = 12.4 dB below the reverberant sound field for the monopole and only 20*log(3/1.24) = 7.7 dB below it for the dipole.
The 4.8 dB lower level of the reverberant field in the
case of the dipole significantly reduces the masking influence of the room upon
sonic detail. It eliminates the sensation of overload of the room during loud
passages of program material and makes your listening sessions much less noisy
to your neighbors.
You have often experienced the poor intelligibility of spoken words from PA
systems in enclosed public spaces. Usually a central cluster of loudspeakers
aims at the audience. In reality the speakers are not very directional and too
much sound is radiated towards useless spaces, only to bounce around and raise
the reverberant sound level. It does not help to increase the volume to obtain
more direct sound, because it also raises the reverberant sound level. Speech
modulation gets lost in this, somewhat like the loss of articulation in my woofer
test signal.
Rooms for multi-channel sound
It has been suggested (R. Walker, BBC, 1998) that the reverberation time T60
over the 200 Hz to 4 kHz frequency range be adjusted to
T60 = 0.3 (V/V0)1/3 [s] where V0 = 100 m3 (11)
with a tolerance of +/-50 ms which is allowed to increase
linearly to +300 ms between 200 Hz and 63 Hz.
The room of Example 2 should thus have T60 = 300 ms +/-50 ms. This
makes for a subjectively quite dead room, which is fine if the room is dedicated
solely to Home Theater and surround sound, but is in my opinion a very
overstuffed environment for normal living. It has the effect of making the
reverberation distance xr = 1.04 m for the monopole and xr
= 1.8 m for the dipole. At a viewing/listening distance of 2 m the direct sound
is only about 6 dB below the reverberant level of the monopole which is good for
sound clarity.
Instead, you could use a dipole, increase T60 to a much more livable
600 ms and have the same direct-to-reverberant ratio as for the monopole for
which the specification was developed.
Amplifier power to obtain Reference Level
When you know the equivalent sensitivity Ls of your speaker in dB SPL at 1 W
(2.83 V across 8 ohm) and 1 m distance and the reverberation time T60 of your room, then
you can estimate the amount of power Pref required to obtain a
specified reference level Lref at the listening distance xl.
First calculate the reverberation distance xr from (10). Then the
level of the reverberant field for 1 W into the speaker is
Lr(1W) = Ls - 20 log(xr) [dB SPL] (12)
If the listening distance xl is greater than xr, then the amplifier power in dBW is
Pref = Lref - {Ls - 20 log(xr)} [dBW] for xl > xr (13)
Example 3
Ls = 89 dB SPL at 1 W, 1 m
Lref = 85 dB SPL
Monopole:
xr = 1.04 m for T60 = 300 ms
Lr(1W) = 89 - 20 log(1.04) = 88.7 dB SPL
Pref = 85 - 88.7 = -3.7 dBW, equivalent to 10(-3.7/10) =
0.4 W
Dipole:
xr = 1.8 m for T60 = 300 ms
Lr(1W) = 89 - 20 log(1.8) = 83.9 dB SPL
Pref = 85 - 83.9 = 1.1 dBW, equivalent to 10(1.1/10) = 1.3
W
With a suggested 20 dB of SPL (= 100 x power) headroom over reference level the monopole requires 40 W and the dipole 130 W to set up a 105 dB SPL reverberant sound field. The dipole's direct sound, though, is 4.8 dB higher than the monopole's and will be 105 - 20 log(3/1.8) = 100.6 dB SPL at 3 m distance. The increased clarity could be traded off for a more lively room with larger T60 and the same 40 W amplifier power and direct-to-reverberant SPL ratio as for the monopole.
Room response time
It takes time to build up the reverberant sound field in a room. Combining
the expressions for rise time (2) and T60 (3) we obtain
Trise = 0.32 T60 [s] (14)
You can think of Trise as the time constant of the room. If music or speech varies faster than the time constant, then the room will not respond fully and you hear predominantly the direct sound from the speaker. For 630 ms reverberation time and 200 ms rise time this covers modulation envelopes of a sound down to 1/200ms = 5 Hz which, in my opinion, is preferable over the 10 Hz envelope rate of a T60 = 300 ms room.
In all practical cases the room response time is large compared to the time it takes a reflected sound to reach the listener and therefore reflections will not be masked by the reverberant field. Depending upon the directivity of the source and the proximity of reflecting surfaces and objects specific absorptive or diffusive treatment may become necessary. It should not be overdone, though, because a certain amount of lateral reflection is subjectively desirable to not destroy the impression of a real space.